実務家がMaterials Informaticsに期待すること 「第1回:MIで実現できること(前半)」

はじめに
なぜ今、実務家がMaterials Informatics (MI) に注目するのか
Materials Informatics (MI)は、「機械学習・AIの力を借りて、材料開発を行う手法」です。 この10年余りの企業での試行錯誤により、MIが材料開発現場で実際に役立つ手法であることが証明されつつあります。 実務家たちの間で「MIは使えるツールである」という認識が広がりつつあることが、私がMIに注目する理由です。
「MIは何ができるのか?」という素朴な疑問の重要性
研究開発の実務において、MIが有用なツールであることを認識している読者も多いでしょう。 しかし、「実際に、MIは何ができるの?(逆に、何はできないの?)」という質問を上長から投げかけられたとき、よどみなく答えられる方はどれほどいるでしょうか。 実務の中で様々な方と話をする際、MIに対する誤解や知識不足に遭遇することが少なくありません。 そういう私自身も、この問いに対して明快に答えることが難しいと感じている実務家の一人です。
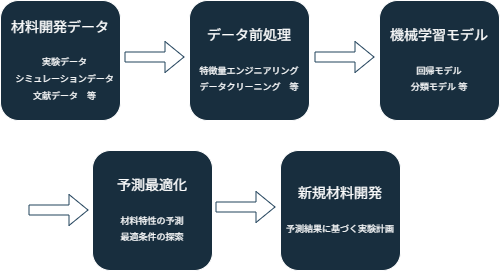
図1: MIの各ステップでの具体的な作業内容と、それらがどのように連携して材料開発を進めるかを示す概念図。データ収集から予測・最適化までの流れを表現。
図1に示す通り、MIは「機械学習・AIの力を借りて、材料開発を行う手法」ですが、特定の技術を用いている以上、必ず得手不得手があります。 そのため、MIを利用する・利用したいと考える者にとって、「MIは何ができるのか?」を事前に理解しておくことは極めて重要です。
しかし、この理解を深めることは簡単ではありません。その理由として、以下の2つが挙げられます:
-
MIは他分野の機械学習・AIと比較しても比較的新しい応用分野であり、信頼できる情報が限られる
-
化学・材料分野は非常に裾野が広く、ある分野でのMI実施例が、自身の研究開発に直接応用できないことが多い
本シリーズの狙い
本シリーズでは、「MIは何ができるのか?」という素朴な疑問に答えるため、様々な角度から考察を行います。 対象読者はMI初心者~中級者を想定しており、MIの初歩的な知識はお持ちであることを前提に話を進めていきます。
シリーズは全5章を予定しています:
- 第1章:MIで実現できること
- 第2章:シミュレーションとの使い分け
- 第3章:MIで「つなぐ」ということ
- 第4章:現状の技術的制約
- 第5章:実務での活用戦略
このシリーズを通じて、読者の皆様がそれぞれの立場から「MIは何ができるのか?」という問いへの答えを見つけられることを願っています。
早速、次のセクションから、「MIの特徴から、具体的にMIは何ができるのか?」について話を進めていきます。
1. MIの本質的な特徴
MIの本質的な特徴は、インフォマティクス(統計的手法)がもつ帰納論的なアプローチにあります。 帰納論とは、「いくつかの個別の事象から一般的な規則・法則を抽出する手法」です。
分かりやすい例として「風が吹けば桶屋が儲かる」ということわざを考えてみましょう:
- 個別の事象:A町、B町、C町で強風が吹いた時、それらの町の桶屋の売り上げが増加した
- 一般的な法則:強い風が吹くと、その町の桶屋の売り上げが増加する
これをMIの文脈で考えると:
- 個別の事象:過去の材料開発データ
- 一般的な法則:新規材料データの特性予測
具体的な例として、ポリマーA、B、Cにそれぞれ添加剤Zを加えると、いずれも耐熱性が向上したというデータから、「ポリマーに添加剤Zを添加すると耐熱性が向上する」という一般的な法則を見出すことができます。 このように一般的な法則を見出すことで、耐熱性材料の開発を効率化できます。
ここで重要な要素の一つが「過去の材料開発データ」です。 そして、そのデータから意味のある一般的な規則・法則を抽出できるかどうかが、MIの成否を分ける重要な要素となります。
図2に示した図は、実験データからある極大値を示す関係性を抽出できたもの(右上)と、出来なかったもの(右下)を対比したものです。 この図からも分かる通り、規則・法則を正しく抽出するには、実験データが、法則の特徴的な箇所全体をカバーできている必要があります。 つまり、MIでは「どんなデータを学習させたのか」が大切だということが分かります。
念のため補足しておくと、機械学習モデルの学習精度(例えば、決定係数(R2)や二乗誤差(MSE)など)は、右上と右下のグラフで大差ありません。 モデルの学習精度は、学習したデータとモデルの予測値との差の大小を取り上げています。 そのため、データが存在しない領域のモデルが、実際の法則に当てはまっているか否かは全く評価していないので、十分に注意してください。
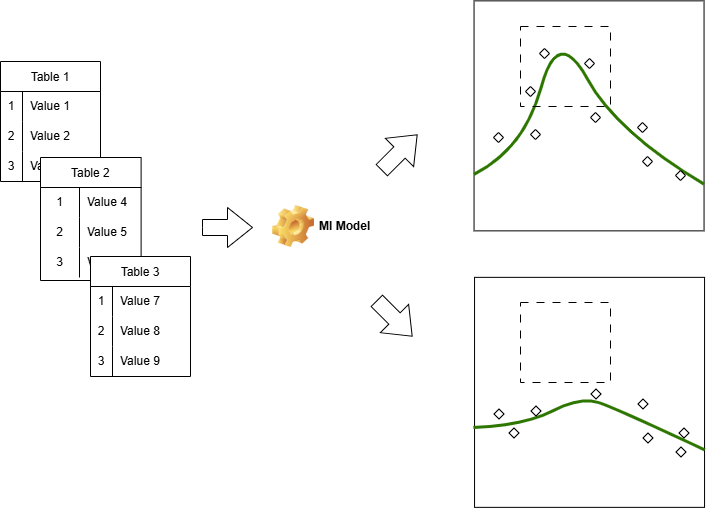
図2: データの質と量が、法則の抽出精度に大きく影響することを示す図。右上は正しく極大値を捉えているが、右下はデータ不足により正しい関係性を抽出できていない例。
それでは、人間とMIで学習方法に違いはあるのでしょうか。 この点を掘り下げてみます。
過去の経験を学び、類似事例に応用できる
私たち人間は、過去の実験結果から、次の実験結果を予測します。 また、過去の研究テーマと似た研究テーマを進める際には、過去の成功例や失敗例を参考に研究計画を立案します。
MIでも同じことが可能です。過去の材料開発データから:
- 実験結果の予測:順解析
- 類似テーマの結果予測:順解析
- 新しい研究計画の立案:逆解析/最適化
1と2では順解析を使い、3では逆解析/最適化という手法を用いています。
人間の経験則との違い
人間とMIの経験則には、どのような違いがあるのでしょうか。 材料開発において、人間とMIは異なる方法で情報を処理します:
人間の場合:
- アナログ的な感覚(五感)を基本とする
- 測定機器からの数値データで補完する
- 直感的に経験則を導き出せる
- 経験の積み重ねで勘を磨く
MIの場合:
- 測定機器からの数値データが基本
- デジタルデータのみを処理する
- 予め決められた手順・アルゴリズムで経験則を導く
- 蓄積されたデータから複雑な関係性を抽出する
現在のMIは、事前に準備されたデータを使い、決められた手順・アルゴリズムに従って経験則を導きます。 そこには、人間と同じように直感や勘を働かせたり、セレンディピティを発揮する要素はありません。
例えば、MIによる「新しい研究計画の立案」では、ガウス過程回帰とベイズ最適化を組み合わせて、不確実性が高い/未探索の領域を優先的に実験することで、確実に最適解にたどり着けるような仕組みを採用しています。 MIは予想外の飛躍が少ない代わりに、確実に論理的に最適解にたどり着くことができるのです。
現時点では、ここが人間とMIの最大の違いだと思います。
MIならではの強み
他にも、MIには以下のような強みがあります:
- 多様な解析手法の活用
- 多様な機械学習モデル:ニューラルネットワーク、決定木、ガウス過程回帰など
- 対象データの拡大:数値、画像、スペクトル、文章などマルチモーダルデータへの対応
- データの記憶と処理
- 大容量・長期間のデータを長期間保持
- 膨大なデータから一貫した経験則を導出
- 複雑な関係性の把握
- 非線形モデルなど複雑な機械学習手法の活用
- 人間には見つけにくい相関関係の発見
機械学習の分野は日進月歩で研究開発が進められており、これまで以上にMIの強みが増すことは疑う余地がありません。
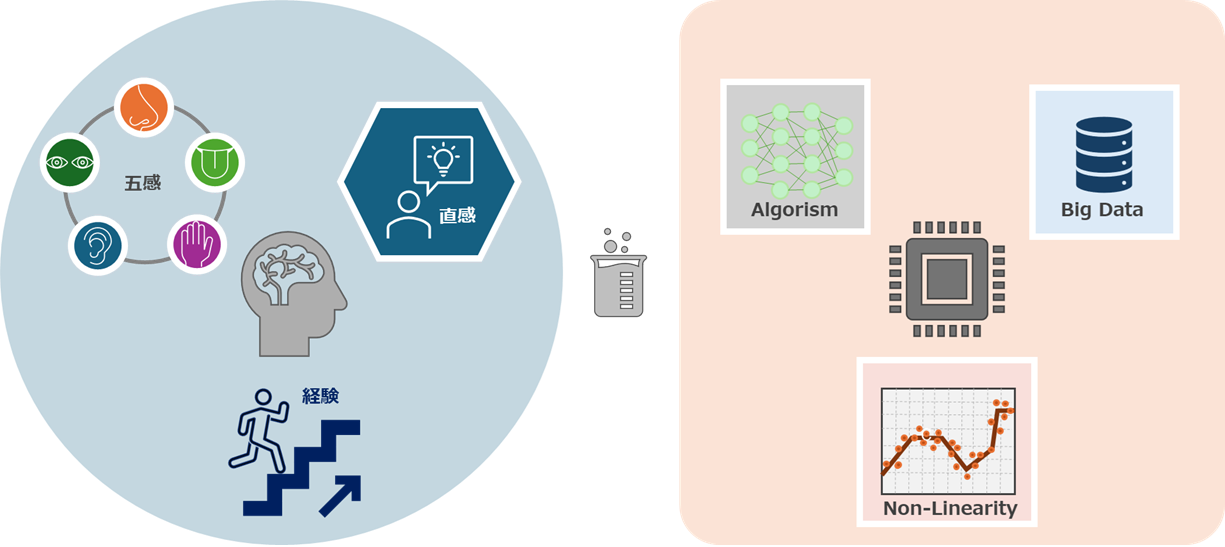
図3: 人間とMIの特徴それぞれが得意とする領域を視覚的に表現した図。左は人間の直感的な経験則、右はMIのデータ駆動型の経験則を示す。
データからの学習とは具体的に何か
「データから学習する」という表現は、これまで述べてきた「規則・経験を抽出する」、「経験則を見出す」、「類似事例を見つける」とほぼ同じ意味です。
機械学習の文脈では、より具体的に以下のように定義されます:
- 学習する事象 → データはデジタルデータ
- 一般的な法則を抽出 → モデル学習(回帰または分類)
つまり、「与えられたデジタルデータから回帰もしくは分類モデルを学習する」ということです。 一見、これは非常に単純で理解しやすい内容のように思えますが、実践では厄介なことが起こり得ます。
例えば、与えられたデータにバイアスや意図しないエラーが含まれている場合、それらの特徴も学習してしまいます。 人間であれば無意識に選別するようなエラーであっても、機械的に選別するのは厄介な場合も存在します。
Kozaの著書に記された、電子回路の自動生成に関する実験を例に挙げましょう[1]。 遺伝的プログラミングを用いて電子回路の設計を自動生成させたところ、人間が準備した模範解答とは異なる回路が得られました。 しかも、その性能は模範解答を上回ります。
これは、電子部品には製造上のばらつき等が存在しており、理想的な電子部品とは異なっていることが原因でした。 つまり、理想的な電子部品を組み合わせた理想回路を出力したのではなく、実物の(非理想的な)電子部品に最適な回路を提案したのです。
このように、人間が意図しようとしまいと、バイアスやエラー込みのデータから回帰や分類の関係性を抽出するのが、機械学習において「データから学習する」ことの意味になります。
データの範囲が学習される範囲
「MIは予測能力がある」と表現すると、「全く未知の材料を発見する能力がある」と勘違いするかもしれません。 しかし、MIにおいて、学習データの範囲から外れる領域の予測精度は全く保証されていません。これに関しては特に注意が必要です。
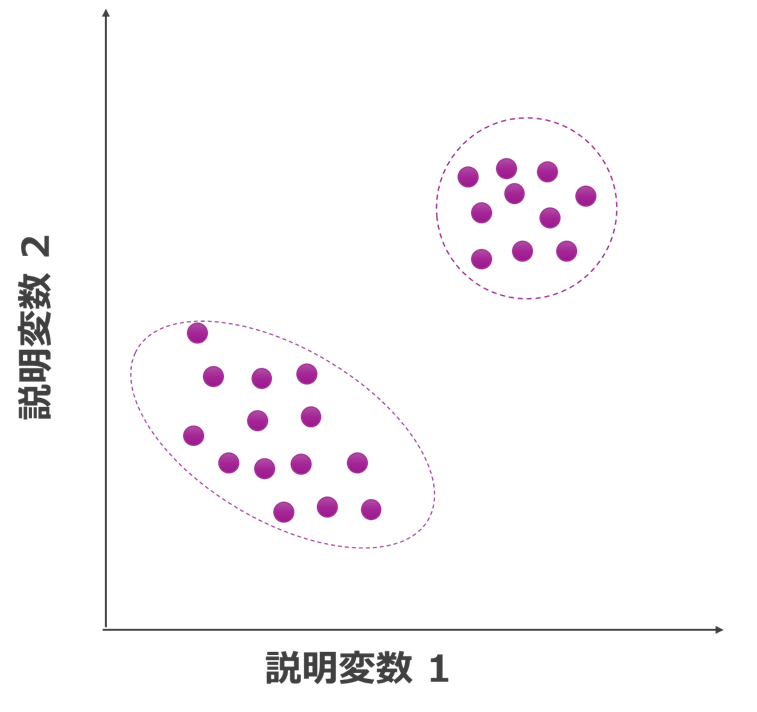
図4: 学習データの分布に基づいて、予測が可能な領域と不可能な領域を視覚的に表現した図。紫色点線部分が学習モデルの適用範囲。
図4に示す通り「学習モデルの適用範囲」と呼ばれる概念が存在します。 大雑把に表現すると、「学習モデルの適用範囲は学習データに近い範囲」です。 シミュレーションなどの理論に依拠した計算にも境界条件(理論の適用範囲)がありますが、それとは異なり、あくまで学習データに近しい入力に対してのみ、精度の高い予測が可能です。
実務での意味:属人的知識の形式知化
属人的知識の保存
実務において、属人的知識をMIに落とし込むことには重要な意味があります:
- 失われやすい属人的知識を長期保存
- 複数人の知識を統合的に蓄積
- 一貫した形での知識活用が可能
昨今、経営・マネジメント層の多くがMIに着目する理由は、日本特有の終身雇用が崩れてジョブ型雇用が台頭したり、人手不足が慢性化することにより、会社固有知識が消失することを危惧しているからではないでしょうか。
失われた知識を取り戻すことは容易ではありません。 従って、属人的知識をMIに落とし込むことは、今や経営課題の一つと言っても過言ではないのかもしれません。
また、近年の材料開発は、必要とされる知識が急速に複雑化しており、関連技術が多岐に渡ります。 もはや、個人が専門家として保持できる知識量を大きく超えています。
複数人の属人的知識をMIに統合的に蓄積し、一貫した形で活用できるようにしておくことが、今後の材料開発では望まれます。
課題と注意点
属人知識を意味ある形で蓄積するには、いくつかの課題があります:
- 人間のアナログ的な感覚をデジタル化する難しさ
- 十分な精度のデータ収集の必要性
- 職人技の場合、現状以上のセンサーデータが必要な可能性
化学分野ではアナログ的な感覚に優れ、直感的に経験則を導き出せる人が多く存在します。 裏を返せば、アナログ的な感覚に優れるが故に、デジタル化データの取得には消極的な場合が多いように思います。 デジタル化に消極的な人からも協力を得て、必要十分な精度のデータ収集に努める必要があります。
2. まとめ
今回は、第1章「MIで実現できること」の前半として、MIの本質的な特徴を詳しく述べました。 改めて要点を箇条書きにすると:
1. MIの基本的な特徴
- 統計的な手法を用いて、学習データから一般的な法則を見出す
- データに含まれるバイアスやエラーも学習する
- データが存在しない部分は学習されない
2. MIで実現できること
- 実験結果の予測(順解析)
- 類似テーマの結果予測(順解析)
- 新しい研究計画の立案(逆解析/最適化)
3. MIの強み
- 多次元の説明変数を用いた学習が比較的容易
- 非線形な関係など、人間が言えにくいパターンの発見が得意
- 属人的知識の保存と活用が可能
4. 実務での注意点
- 人間とMIの違いを意識したデータ取得が必要
- 通常のMIで学習できるのは相関関係であり、因果関係は学習できない
- 学習データの範囲を超えた予測は信頼性が低い
次回
次回は、第1章「MIで実現できること(後半)」をお届けします。 データから具体的に何が学べるのか、MIを実践で扱う際の注意点などを述べる予定です。
参考文献
- Koza, J. R. (1992). Genetic Programming: On the Programming of Computers by Means of Natural Selection. Complex Adaptive Systems.