前回の振り返り

初回となる前回は、「MIの本質的な特徴」から俯瞰して「MIは何ができるのか？」について考えました。 主なポイントは以下の通りです：

1. MIの基本的な特徴
   • 統計的な手法を用いて、学習データから一般的な法則を見出す
   • データに含まれるバイアスやエラーも学習する
   • データが存在しない部分は学習されない
2. MIで実現できること
   • 実験結果の予測（順解析）
   • 類似テーマの結果予測（順解析）
   • 新しい研究計画の立案（逆解析／最適化）
3. MIの強み
   • 多次元の説明変数を用いた学習が比較的容易
   • 非線形な関係など、人間が言えにくいパターンの発見が得意
   • 属人的知識の保存と活用が可能
4. 実務での注意点
   • 人間とMIの違いを意識したデータ取得が必要
   • 通常のMIで学習できるのは相関関係であり、因果関係は学習できない
   • 学習データの範囲を超えた予測は信頼性が低い

今回は、これらの特徴をさらに深堀することで、MIが具体的に何を学べるのか、そして実務でどのように活用すべきかについて詳しく説明します。 特に、データから学べる関係性の種類や、実務での活用における重要な心構えに焦点を当てていきます。

1. データから何を学べるのか

前回は学習データに焦点を当てましたが、ここでは学習モデルに関連した話をします。MIの本質的な特徴を理解するために、まず「相関関係の学習」から始めましょう。

データ項目間の相関性を学習する

機械学習の学習モデルは、回帰または分類モデルを出力しますが、回帰モデルで学習されるのは「相関」であって「因果」ではありません。この違いを理解することは、MIを実務で活用する上で非常に重要です。

具体例で話をします。

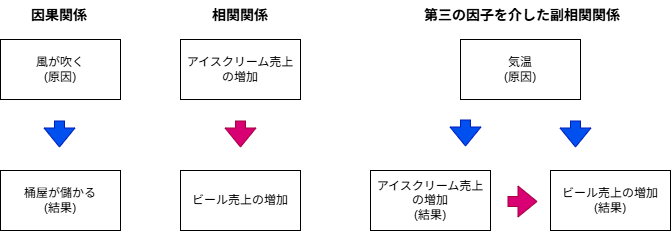
• 「風が吹けば桶屋が儲かる」
• 「教会が多い地域は、殺人件数が多い」
• 「アイスクリームの売り上げが伸びる日は、ビールの売上も伸びる」

ことわざによると（諸説あるようですが）、「風が吹く」ことと「桶(棺桶)の売上」には因果関係があります（相関関係もある）。 それでは、他の2つの話に、因果関係はあるでしょうか。 これら2つには、相関関係は存在しても、おそらく因果関係はありません。

詳しくは割愛しますが、これら2つの例は、第三の共通変数を介した副相関関係にあります。 「教会の数」と「殺人件数」は『人口』を介した相関だと考えられます。 どちらも、人口が多い場所で増える傾向にあります。 同様に、「アイスクリームの売上」と「ビールの売上」は『気温(季節)』を介した相関を見ています。

ここで挙げた例は単純ですが、実際の材料開発で複数の要素が複雑に絡み合っている場合、因果を捉えられたのか、単に相関を見ているのか判別は難しいです。 一番重要なことは、通常の機械学習において、因果関係を捉えているように見えても、「論理的には何も保証されていない」ということです。

材料開発における具体例を挙げると：

• 「添加剤の量を増やすと材料の強度が上がる」という相関関係は、実は「添加剤の分散性」という第三の要因によって説明される可能性がある
• 「製造温度を上げると収率が上がる」という相関関係は、実際には「反応速度」と「副反応の進行」のバランスによって決まる

なお、因果関係に関する研究分野として「因果推論」や「有向グラフを用いたグラフ理論」などが存在し、一部では有用性が確かめられていますが、実践的なMIで容易に使えるレベルではないと感じています。

なお、因果関係に関する研究分野として「因果推論」や「有向グラフを用いたグラフ理論」などが存在し、一部では有用性が確かめられていますが、実践的なMIで容易に使えるレベルではないと感じています。

単純な1対1の関係を超えた発見

先程は3つの単純なたとえ話（説明変数と目的変数が一つずつ）を例に説明しましたが、MIの真価は、このような単純な関係を超えた複雑な関係性の発見にあります。

材料開発において、複数の物理的・化学的特性を満たす材料を探索することは珍しくありません。 そして複数の目的変数を満たす機械学習モデルの構築を、同じ説明変数を用いて構築することが可能です。

多数の説明変数が存在しても構いませんが、注意も必要です。 製造工程が複数にまたがる場合、主要な変数を抜き出すだけでも100～500程度あるという話はよく聞きます。 仮に説明変数が100ある場合、次元の呪いを克服する必要があり、相当な数のデータが必要となります。 データ数が不足し、次元の呪いが実務上の障害になる場合は、主成分分析やt-SNEなどの次元削減方法を用いるなどの回避策が必要です。

比較として、理論的な解析を行う場合を考えてみます。 理論を実務に適用するには[1]：

• 理論に関係する説明変数を選別
• 理論式を変形して目的変数と説明変数の関係を構築する
• 境界条件（理論適用の限界点）を加味した繊細な実験デザインを考える
  • 理論上複数の説明変数の存在が考えられる場合は、一つの説明変数だけが変化するよう実験をデザインし実行する
• 実験結果と理論式が実験誤差範囲内で一致することを確認する

このように、理論を実務に適用するには、とても手間がかかる確認を必要とします。 そして、この操作を、目的変数の数だけ実施する必要があります。 また、多くの場合、複雑な材料系には理論は当てはまりません。

その点、MIは関連する可能性がある説明変数を全て加えて学習することができます。 どの変数が重要なのかは、学習結果により示されます。

適切な学習データが揃ってさえいれば、機械学習モデルが複雑な非線形な関係性を発見してくれます。

2. MIを活用する際の心構え

これまで説明してきた「データから学べる関係性」の特徴を踏まえると、MIを実務で効果的に活用するためには、いくつかの重要な心構えが必要になります。特に、相関関係の学習や多次元データの扱い、非線形関係の発見といった特徴を最大限に活かすためには、適切なデータの取り扱いと学習範囲の理解が不可欠です。

以下に、これまで説明してきた内容を実務で活用する際の5つの重要な柱を示します。

データの質と量への意識

MIの本質は「データからの学習」にあります。先ほど説明した相関関係の学習や多次元データの扱い、非線形関係の発見といった特徴を活かすためには、以下の点に常に意識を向ける必要があります：

• データの質
  • 測定機器からの数値データの精度と信頼性
    • 例：材料の強度測定における試験条件の標準化
    • 例：熱分析における測定条件の制御
  • 人間のアナログ的な感覚のデジタル化の適切性
    • 例：材料の評価基準の統一
    • 例：定量的な評価方法の確立
  • バイアスやエラーの存在とその影響
    • 例：測定者による評価のばらつき
    • 例：装置の状態による測定値の変動
• データの量
  • 説明変数の数に対する十分なデータ数の確保
  • 次元の呪いを考慮したデータ収集計画
    • 例：重要な変数に絞った実験計画の立案
    • 例：段階的なデータ収集による効率的な学習
  • 組織の知的資産として活用可能な範囲の確保
    • 例：過去の実験データの体系的な整理と活用
    • 例：部門間でのデータ共有の仕組みづくり

学習範囲の理解と活用

先ほど説明したように、MIの予測能力には明確な境界があります。特に、非線形関係の発見や多次元データの扱いにおいて、以下の点を意識する必要があります：

• 学習データの範囲内での予測精度の保証
• 未知領域への予測の限界の認識
• 理論的解析との使い分けの重要性

属人的知識の形式知化への取り組み

材料開発の高度化に伴い、以下の点が重要になります：

• アナログ的な感覚のデジタル化
  • 適切なセンサーデータの取得
  • 測定機器の選定と精度管理
  • デジタルデータの体系的な蓄積
• 組織的知識の構築
  • 複数人の知識の統合
  • 分野横断的な知識の統合
  • 一貫した形での知識活用

相関と因果の区別

先ほど詳しく説明した相関関係と因果関係の違いを、実務で適切に扱うために：

• 相関関係と因果関係の区別
• 第三変数を介した副相関の可能性の考慮
• 理論的知見との組み合わせの重要性

実務での活用戦略

これまで説明してきた特徴を活かした実践的な活用のために：

• データ収集の計画的な実施
  • 必要なデータ項目の特定
    • 例：材料開発の目的に応じた測定項目の選定
    • 例：品質管理に必要な特性値の明確化
  • 収集プロセスの標準化
    • 例：実験手順の文書化
    • 例：データ入力フォーマットの統一
  • データ品質の管理
    • 例：測定機器の校正
    • 例：異常値の検出と対応
• 学習モデルの適切な選択
  • 線形・非線形モデルの使い分け
    • 例：単純な関係には線形モデル
    • 例：複雑な関係には非線形モデル
  • 次元削減手法の活用
    • 例：主成分分析による変数の整理
    • 例：t-SNEによる可視化
  • モデルの解釈可能性の考慮
    • 例：決定木による予測
    • 例：変数の影響度の可視化
• 継続的な改善
  • 学習結果の検証と改善
    • 例：モデルの評価
    • 例：予測誤差の分析
  • 新規データの追加とモデルの更新
    • 例：モデルの再学習
    • 例：新しい知見の反映
  • 組織的な知識の蓄積と活用
    • 例：成功事例の共有
    • 例：失敗事例からの学習

ここに挙げた各項目は教科書的な内容ばかりですが、これらを適切に実践できる能力を持つことが、今後の実務家や組織に求められています。

3. まとめ

MIでできることの整理

「MIは何ができるのか？」という主題のもと、前回と今回の2回にわたって説明してきました。全体を整理すると以下のようになります：

1. MIの基本的な特徴と実現できること（前回の内容）
   • 統計的な手法による一般法則の抽出
   • 実験結果の予測（順解析）
   • 新しい研究計画の立案（逆解析／最適化）
   • 属人的知識の保存と活用
2. データから学べる関係性（今回の内容）
   • 相関関係の学習（因果関係ではない）
   • 多次元の説明変数を用いた複雑な関係性の把握
   • 非線形な関係や人間には見えにくいパターンの発見
   • 複数の目的変数を同時に扱う能力
3. 実務での活用における重要な柱
   • データの質と量への意識
   • 学習範囲の理解と活用
   • 属人的知識の形式知化への取り組み
   • 相関と因果の区別
   • 実務での活用戦略

これらの特徴を踏まえると、MIは材料開発において以下のような価値を提供します：

• 効率化: 実験結果の予測による開発時間の短縮
• 発見: 人間の直感では見つけにくい関係性の発見
• 知識の継承: 属人的知識の形式知化による組織的活用
• 複雑な最適化: 複数の説明変数と目的変数を同時に考慮した材料設計

実務家へのメッセージ

これまでの説明を踏まえ、MIを実務で活用する際の重要なポイントを整理します。技術的な知識や手法の理解はもちろん重要ですが、それ以上に重要なのは「MIの本質を理解し、適切に活用する」という姿勢です。

1. MIの特徴を理解する
   • 相関関係の学習が基本であることを認識
   • 多次元データの扱いにおける次元の呪いへの対応
   • 非線形関係の発見におけるMIの強み
2. 実務での活用方法を考える
   • データの質と量を確保するための計画的な取り組み
   • 学習範囲を理解し、適切な予測を行う
   • 属人的知識の形式知化による組織的活用
3. 継続的な改善を意識する
   • データ収集プロセスの標準化と改善
   • 学習モデルの適切な選択と評価
   • 組織的な知識の蓄積と活用

これらの点を意識することで、MIを単なる「ツール」としてではなく、材料開発を革新する「戦略的な武器」として活用することができます。

次回予告：シミュレーションとの使い分け

次回は、MIとシミュレーションの特徴を比較し、それぞれの強みを活かした使い分けについて説明します。特に、理論的な解析とMIの組み合わせ方について、具体的な事例を交えながら解説する予定です。

参考文献

1. 奥村 剛 (2020). 印象派物理学入門: 日常にひそむ美しい法則. 株式会社日本評論社

用語解説

• 因果推論: 変数間の因果関係を統計的に推測する手法。相関関係と因果関係を区別し、真の因果関係を特定することを目的とする。

• 有向グラフ: ノード間の関係性を矢印で表現するグラフ。因果関係を表現する際に用いられる。

• 転移学習: ある領域で学習した知識を別の領域に応用する機械学習の手法。

• Knowledge Graph: 知識をグラフ構造で表現し、概念間の関係性を明示的に記述する手法。